Adu domba

Wahai saudara-saudara, mengadu domba adalah hal yang dilarang. Membuat dua pihak yang awalnya rukun dan damai menjadi bermusuhan dan saling bertikai.

Tetapi mengadu domba yang ini sudah menjadi kegiatan rutin orang-orang di daerah Jawa Barat yaitu Garut.
Ya adu domba. Dua domba berlari dari dua arah yang berlawanan mendekat sambil mengarahkan tanduknya ke arah lawan. Dan .......bummmm! Waduuh tidak terbayang pusingnya kepala ini kalau kita bisa merasakannya. Wahai para peng-adu domba ....apakah anda tidak belajar momentum?

Datanya adalah sebagai beikut:
Domba hitam dengan massa 110 kg berlari dengan kecepatan 65 km/jam dan domba putih dengan massa 115 kg berlari dengan kecepatan 50 km/jam.
Jika kedua domba diasumsikan menempel sesaat setelah tumbukan, berapa kecepatan akhir tumbukan dan ke arah mana?

Mengencangkan baut

Suatu baut ban mobil harus dikencangkan sebesar 85 Nm. Hitung gaya F yang harus diberikan jika sudut = 35 derajat, dan d = 420 mm.

Berkenalan dengan momen

Sejauh ini kita sudah mengenal gaya sebagai suatu tarikan atau dorongan terhadap suatu benda. Jika tarikan atau dorongan itu memiliki lengan terhadap obyeknya, maka dikatakan kita memberikan momen pada benda itu.
Sebagai contoh, untuk membuka baut, kita memberikan momen dan bukan gaya langsung. Momen terjadi karena adanya perkalian gaya dengan lengannya.

Bisa anda sebutkan aktifitas-aktifitas lain yang melibatkan momen dan bukan gaya langsung?

Jagoan momentum beraksi

Sang jagoan momentum tidak berdaya jika ada orang yang berdiri di tengah rel kereta api (sengaja ataupun tidak sengaja). Walaupun jaraknya masih ratusan meter, sang masinis tidak berdaya. Kenapa?

Makin besar momentum, makin besar pula usaha (effort) yang harus dilakukan untuk menghentikannya.
Jangankan orang, obyek lain yang lebih besar pun tak berdaya menghadapinya.

Jadi waspadalah bila berhadapan dengan si jagoan momentum ini.

Jagoan momentum

Berikut adalah gambar kereta api super cepat Trains à Grande Vitesse (TGV) atau High Speed ​​Trains.
Maksimum kecepatannya 515.3 km/h (wow!). Beratnya keseluruhan sekitar 400 ton (wow lagi) dengan panjang sekitar 200 m.

Kalau kita kalikan massa TGV dengan kecepatan maksimumnya, maka didapat angka 400.000 (kg) x 515.300 m/(3600 det) = 57.255.556 kg.m/det (wow..wow).

Angka sebesar kira kira 57 juta kg.m/det tersebut adalah besar momentumnya.

Bisa anda bayangkan bagaimana menghentikan sistem dengan momentum sebesar itu?

Berkenalan dengan Momentum

Momentum didefinisikan sebagai perkalian massa kali kecepatan. Suatu benda yang memiliki massa m dan kecepatan v akan memiliki momentum sebesar mv. Makin cepat suatu benda seperti peluru, bola tenis yang telah dipukul, maka makin besar momentumnya. Makin besar massa suatu sistem seperti bis kota, kapal selam, makin besar momentumnya. Jika kedua variabel (massa dan kecepatannya) sama-sama besar, misalkan jumbo jet A380, atau kereta api super cepat maka makin ekstrim lah nilai momentumnya. Suatu sistem dengan momentum besar, makin sulit dihentikan. Butuh gaya eksternal yang besar dapat menghentikannya.

Apa yang terjadi jika suatu sistem dengan momentum besar dihentikan tiba-tiba?

Mengamati Posisi 2 buah traktor

Dua buah traktor siap berkompetisi.

Posisi dua buah traktor yang diamati oleh orang ke tiga sebagai fungsi waktu diperlihatkan pada gambar berikut. Apa saja yang bisa anda simpulkan dari pengamatan ini?

Fenomena menggelinding

Tinjau dua silinder. Yang satu pejal yang satu berongga. Menurut anda, mana yang lebih dulu tiba di bawah? Bagaimana penjelasannya?

Gerak harmonik dengan menggunakan pegas

Suatu pegas yang diberi massa pemberat di salah satu ujungnya sementara ujung lain ditempelkan pada dinding. Ingat karakteristik pegas? Pegas jika diberi gaya atau simpangan entah itu dalam arah tarik atau tekan akan berusaha untuk melawan. Jika dia ditarik maka akan melawan dengan berusaha menarik kembali ke arah semula. Sebaliknya jika dia ditekan, maka pegas akan menekan balik.

Jika pegas diberi simpangan sebesar –A (ke arah bawah) seperti pada Gambar, maka dia akan memiliki energi potensial sebesar Ep = ½ kx2. Karena hukum kekekalan energi dan jika gesekan dengan udara diabaikan, maka pada posisi awal/keseimbangan, Ep nol dan Ek maksimum sehingga massa berusaha untuk terus bergerak ke atas sampai mencapai simpangan maksimum A (arah atas). Pada simpangan maksimum tersebut, Ek nol dan Ep maksimum sehingga pegas berusaha kembali ke bawah dan seterusnya.
Seperti tadi sudah disebutkan, jika gesekan sistem dengan udara diabaikan dan tidak ada gaya eksternal lain yang bekerja, maka idealnya sistem akan bergerak terus-menerus.

Gaya ada di mana-mana

Tahukah anda, anda tidak bisa menghindar dari gaya dalam kehidupan sehari-hari. Anda secara rutin menggunakan gaya bahkan tanpa anda sadari. Saat anda menyebrangi jembatan, berjalan di atas tanah, mengangkat burger dan memasukkannya dalam mulut, memutar tutup kaleng selai, mengedipkan mata pada pacarmu, membuka pintu, menekan papan ketik di laptop anda, mengendarai mobil, memanjat tangga, mengeluarkan dompet, bahkan bernafas atau berkata.
Gaya terintegrasi dalam hidup kita untuk menggerakkan suatu obyek.
Dengan fisika, anda akan memahami fenomena tentang gaya tersebut.

Bertemu dengan Mr. M, L dan T

Halo apa kabar perkenalkan teman-teman kita Mr M, Mr. L dan Mr.T.
Ya mereka adalah leluhur dari besaran fisik. M adalah Massa, L adalah Panjang (Length) dan T adalah Waktu (Time).

Besaran-besaran fisik yang lain adalah keturunan dari Mr. M, L dan T.
Coba kita lihat:
[Volume] (dibaca satuan volume) = L pangkat 3
[Kecepatan] = L/T
[Tekanan] = M /[(L kuadrat) kali (T kuadrat)]

Gaya gesek statis dan kinetis

Suatu balok awalnya berada dalam keseimbangan seperti diperlihatkan pada Gambar (a). Kemudian jika kita beri gaya P, gaya gesek F berusaha menyeimbangkan sehingga sistem tetap diam. Jika P diperbesar, maka F pun menyesuaikan ikut membesar seperti ditunjukkan oleh Gambar (b). Sampai suatu saat terdapat P dimana gaya gesek maksimum Fm. Di bawah Fm, koefisien geseknya adalah koefisien gesek statis. Jika P besarnya diatas Fm, maka balok tidak bisa lagi menyeimbangkan sehingga akhirnya bergerak. Koefisien geseknya adalah koefisien gesek kinetis.

Soal Tegangan tali

Suatu bola pejal dengan massa 1 kg digantung pada tali seperti diperlihatkan pada Gambar berikut. Jika sistem berada dalam kesetimbangan, hitung tegangan tali T1 dan T2.

Dimanakah kamu berada?

Dimanakah kamu tinggal? Saya tinggal di jalan Kesehatan 3 (misalnya). Dimanakah itu? Jakarta Pusat. Sebelah mana? Dekat monas. Ke arah mana dari Monas?
Yah begitulah pertanyaan-pertanyaan yang diajukan orang yang menanyakan alamat rumah.
Di jaman sekarang ini, di era Global Positioning System (GPS), mestinya tidak perlu pertanyaan macam-macam. Jika kendaraan kita dilengkapi dengan alat GPS, maka kita dapat menemukan alamat rumah tanpa perlu bertanya kesana kemari. Kenapa bisa?

Bumi, tempat kita tinggal ini, telah memiliki koordinat (garis-garis imajiner, yang didefinisikan orang) yang terdiri dari garis lintang (Latitude) dan garis bujur (longitude). Garis lintang merupakan lingkaran-lingkaran yang membagi bumi menjadi utara dan selatan. Lingkaran nol (ekuator) merupakan garis khatulistiwa (tentu kita kenal kan). Indonesia dilalui garis khatulistiwa. Garis bujur merupakan garis yang membagi bumi menjadi sisi barat dan sisi timur. Batas 0 adalah Greenwitch Mean Time (GMT) sebuah lokasi di Negara Inggris.

Pengamatan Ayunan Newton

Anda pernah melihat benda seperti di bawah ini? Benda ini biasanya menjadi pelengkap pajangan di meja kerja. Lima bola baja digantung sebaris pada sebuah tumpuan yang berupa lengkungan baja juga. Jika bola baja yang paling kiri diberi simpangan kemudian dilepas, maka bola paling kiri akan menumbuk bola di sebelah kanannya. Maka yang terjadi adalah tumbukan itu ditransfer sehingga bola yang paling kanan akan bergerak dan membentuk simpangan yang relatif sama dengan simpangan awal. Mengapa hal ini bisa terjadi?

Bagaimana kalau dua bola yang disimpangkan?

Soal Batang kantilever

Batang kantilever sering kita lihat dalam kehidupan sehari-hari. Lihat peloncat indah yang sedang beraksi di kolam renang

Berikut contoh soal batang kantilever yang ditumpu tetap (fixed) pada salah satu ujungnya dan dikenai gaya F1, F2, F3 dan beratnya sendiri.

Maka DBB untuk sistem ini adalah

Soal batang 2 gaya

Batang dua gaya atau lebih dikenal dengan istilah Truss adalah batang yang mengalami gaya tarik atau tekan saja. Truss banyak kita lihat dalam kehidupan sehari-hari. Anda tentu pernah melihat sebuah crane di lokasi-lokasi pembangunan.

Berikut adalah contoh struktur truss sederhana yang ditumpu di dua titik A (pin) dan B (roll) dan sebuah gaya di P.

Maka DBB dari sistem tersebut adalah

Koordinat Kartesian dan polar

Koordinat kartesian mempunyai relasi/hubungan dengan koordinat polar sebagai berikut. Tinjau suatu titik P dalam koordinat kartesian dengan koordinat (x, y). Maka P jika dinyatakan dalam koordinat polar dinyatakan dengan (r, theta). Relasinya adalah x=rcos(theta) dan y=rsin(theta).

Mengenal Horsepower

Cerita berawal ketika Watt mengamati seekor kuda poni pengangkat batu bara di sebuah pertambangan. Dia mau menghitung kemampuan kuda poni tersebut dalam bekerja. Dia menemukan bahwa dalam rata-rata, sebuah kuda poni dapat melakukan kerja 22.000 foot-pound dalam semenit. Dia kemudian mengalikan angka tersebut dengan 50% dan mendefinisikan 1 HP sebagai kemampuan melakukan kerja 22000 foot-pound dalam satu
menit.

Jadi 1 HP bisa berarti kemampuan menaikkan 330 pound batu bara setinggi 100 feet
dalam semenit, atau 33 pound setinggi 1000 feet, atau 1000 pound setinggi 33 feet.
Apapun kombinasinya selama jumlah perkaliannya 33000 foot-pound maka itu akan setara daya 1 HP. Tentunya kondisi ekstrim agak sulit merealisasikannya misalnya
meminta kuda poni mengangkut 1 pound setinggi 33000 feet atapun sebaliknya mengangkut 33000 pound setinggi 1 feet. Sangat tidak berperikebinatangan!

Kabel SUTET dan gaya terdistribusi

Pernah melihat kabel tegangan tinggi? Mengapa kabelnya melengkung? Kabel melengkung karena massanya cukup signifikan sehingga kabel mengalami beban terdistribusi sepanjang kabel tersebut.

Panjat pinang dan gaya gesek

Tentunya kita pernah melihat panjat pinang. Yang membuat permainan panjat pinang menarik adalah licinnya pohon pinang. Tentunya menjadi tidak fun lagi kan kalau pohonnya tidak licin. Pohon pinang diberi minyak pelumas agar koefisien geseknya seminimum mungkin sehingga gaya gesek pun menjadi minim.

Pengaruh sudut awal terhadap gerak parabolik

Pernahkan anda menyiram tanaman dengan menggunakan selang? Pernahkah pula anda secara tanpa sadar mengatur-atur sudut selang sehingga lintasan paraboliknya berubah.
Tahukah anda pada sudut berapa jarak horisontal yang dicapai air paling jauh?

Memahami gerak parabolik

Gerak parabolik banyak kita dapati sehari-hari. Gerak parabolik terjadi karena suatu benda dipengaruhi percepatan gravitasi.

Jika diuraikan dalam komponen kecepatan arah horisontal (x) dan vertikal (y), maka seperti tampak pada Gambar berikut

Dalam arah x, kecepatan adalah konstan sementara arah y bervariasi karena ada percepatan gravitasi. Kecepatan awal arah y adalah maksimum. Makin tinggi makin berkurang hingga mencapai nol di puncak. Setelah mencapai puncak, kecepatan arah y berbalik arah. Makin ke bawah makin besar sampai mencapai maksimum saat menyentuh tanah lagi.

Memahami konsep Kerja

Kerja (W) didefinisikan sebagai gaya kali jarak atau gaya kali lintasan. Suatu benda, misalnya buku, jika diberi gaya (F) maka posisinya akan berpindah dari A menjadi di B. Maka definisi kerja adalah tergantung lintasannya. Jika buku pindah posisi dari A ke B melewati lintasan lurus (warna biru), maka kerja yang dilakukan adalah lebih kecil dibanding jika melewati lintasan berbentuk setengah lingkaran (warna coklat).
Logis bukan?

Eksperimen 1: Penentuan koefisien gesek

Tujuan eksperimen ini adalah untuk mendapatkan koefisien gesek koin pada papan tripleks dan koin pada papan kaca. Pada eksperimen ini akan diamati fenomena gesekan antara koin dengan papan landasannya.

Bahan eksperimen:
1.Dua buah koin uang yang berbeda
2.Papan triplek
3.Kaca

Prosedur percobaan
1.Ukur sisi panjang papan tersebut (nyatakan dengan L)
2.Sebuah koin diletakkan di atas papan
3.Perlahan-lahan papan diangkat pada salah satu sisinya.
4.Catat pada ketinggian berapa koin tersebut tepat akan jatuh
5.Hitung sudut dan mu dengan mengacu kepada landasan teori.

Tuliskan hasil percobaan pada Tabel berikut:

Eksperimen 1 memiliki beberapa fenomena mekanika:
1.Benda yang dipengaruhi percepatan gravitasi cenderung bergerak ke tempat yang lebih rendah
2.Terdapat gesekan antara koin dengan papan yang mampu menahannya pada posisi semula sampai ketinggian tertentu.

Tebak arah kecepatan

Sebuah mobil sedang bergerak di sebuah belokan.

Pilih mana vektor kecepatan yang cocok untuk posisi mobil di 1 dan di 2.

Jawaban:
Posisi 1 vektornya adalah .... (Jawaban pilih dari a sampai g)
Posisi 2 vektornya adalah .... (Jawaban pilih dari a sampai g)

Memahami kurva posisi

Tinjau suatu sedan yang bergerak. Setiap 10 detik, posisinya dicatat dan ditandai dengan huruf A sampai F seperti diperlihatkan dalam Gambar berikut. Penentuan posisi Nol sebagai titik referensi adalah bebas, sama seperti Jalan Tol memiliki kilometer nol. Sebelah kanan titik Nol adalah posisi Positif, sebelah kiri posisi Nol adalah posisi Negatif.

Jika kita buat sistem koordinat Kartesian dengan sumbu horisontalnya adalah waktu (t) dan sumbu vertikalnya adalah posisi dalam x (m) maka plot dari posisi mobil sebagai fungsi waktu diperlihatkan pada Gambar berikut:

Apakah anda sudah bisa memahami hubungan antara posisi mobil tersebut dengan kurva posisinya?

Sifat komutatif penjumlahan vektor

Dua buah vektor A dan B dapat memenuhi hukum komutatif penjumlahan A + B = B + A = R

Soal konversi radian ke derajat

Diketahui sudut-sudut berikut dalam satuan radian. Isikanlah titik-titik sebelahnya dengan satuan derajat yang setara.

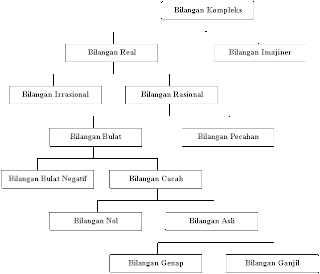
Berkenalan dengan Bilangan

Awalnya bilangan 1, 2, 3, ... dan seterusnya. Bilangan ini disebut bilangan asli.

Jika bilangan itu habis dibagi 2 atau kelipatan 2 maka disebut bilangan Genap.
Jadi bilangan genap itu 2, 4, 6, 8, ...
Jika tidak habis dibagi 2 maka dinamakan bilangan Ganjil.
Jadi bilangan Ganjil itu 1, 3,5,7,9, ...
Jika dilakukan operasi pengurangan misalnya 2-2=0, maka bilangan asli ditambah 0 menjadi bilangan cacah.
Jadi bilangan cacah itu 0, 1, 2, 3, ...
Jika bilangan yang lebih kecil dikurangi yang lebih besar misalnya 2-5 maka hasilnya adalah -3 maka itu adalah bilangan negatif, jika digabung dengan bilangan cacah, maka menjadi bilangan bulat.
Jadi bilangan bulat itu ..., -3, -2, -1, 0, 1, 2, 3, ...
Jika bilangan bulat dibagi bilangan bulat lainnya dan hasilnya tidak bulat, misalnya 3/2=1.5, ¾=0.75, maka kelompok bilangan tersebut adalah bilangan pecahan.
Jadi bilangan pecahan contohnya: ½, ¼, 2¼ , 0.75, 1.25 dst
Gabungan bilangan pecahan dan bilangan bulat disebut bilangan rasional.
Jika bilangan asli diakarkan dan hasilnya bukan bilangan rasional maka disebut bilangan irrasional. Misalnya bilangan pi=3,14159265..., e=2.71828183, akar 5 dst
Gabungan bilangan rasional dan irrasional adalah bilangan real.
Jika didalam akar terdapat bilangan bulat negatif, maka hasilnya adalah bilangan imajiner. Akar -5 = 5i.
Jadi bilangan imajiner contohnya adalah 2i, -0.5i, 100i dst
Gabungan bilangan real dan imajiner adalah bilangan kompleks.